Overview

While trigonometry can be intimidating to some, it need not be, as long as we start with the concept of similar triangles—that is, any 2 triangles with the same proportions between all 3 side lengths have the same interior angles, and any 2 triangles with the same 3 interior angles have the same proportions between side lengths.

Right triangles

Figure 1: Right triangle used to define basic trigonometric relationships.

Trigonometric functions are initially defined in terms of the angles and sides in a right triangle, for acute angles only—i.e. in the interval $\left [ 0, \pi / 2 \right )$. By convention, each vertex is identified by an upper-case letter (most commonly, A, B, and C, for the two acute angles and the right angle, respectively), with the side opposite identified by the same letter, but lower-case. Note that an upper-case letter denotes not only a vertex, but the measure of the angle at that vertex; similarly, a lower-case letter refers not only to the side itself, but to the length of that side. Finally, the right angle is identified by a small square at vertex C.

All of the definitions in the following table are in reference to the triangle in figure 1, above.

Measure	Definition	Java method
Sine	$\sin A = \dfrac{a}{c}$	double Math.sin(double angle)
Cosine	$\cos A = \dfrac{b}{c}$	double Math.cos(double angle)
Tangent	$\tan A = \dfrac{a}{b}$	double Math.tan(double angle)
Arcsine	$\arcsin \dfrac{a}{c} = A$	double Math.asin(double ratio)
Arccosine	$\arccos \dfrac{b}{c} = A$	double Math.acos(double ratio)
Arctangent	$\arctan \dfrac{a}{b} = A$	double Math.atan(double ratio)
Pythagorean theorem	$c = \sqrt{a^2 + b^2}$	double Math.hypot(double a, double b)

Polar coordinates

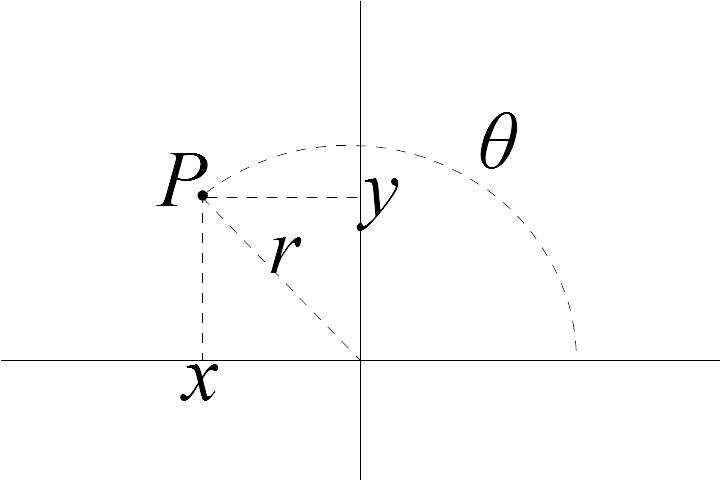Figure 2: Position of point $P$ shown in polar and Cartesian coordinates.

The position of a point $P$ on a plane is usually expressed either with respect to the $X$ and $Y$ axes—that is, in Cartesian coordinates—or with respect to a pole (coincident with the origin of the Cartesian coordinate system) and a polar axis (coincident with the positive $X$ axis of the Cartesian coordinate system). The coordinates used in the latter case are called polar coordinates, and consist of a distance, $r$, measured from the pole, and an angle, $\theta$, measured counter-clockwise from the polar axis. When $\theta$ is in the interval $\left [ 0, \pi / 2 \right )$, the $x$, $y$, and $r$ values form a right triangle, where $\theta$ is the angle opposite $y$. Recognizing this, we can extend the trigonometric relationships beyond acute angles in an intuitive fashion, by expressing them in terms of polar and Cartesian coordinates, allowing $x$ and $y$ to take negative values, and allowing $\theta$ to take values outside the interval $\left [ 0, \pi / 2 \right )$.

All of the definitions in the following table are in reference to the polar and Cartesian coordinate system used in the example shown in figure 2, above.

Measure	Definition	Java method
Sine	$\sin \theta = \dfrac{y}{r}$	double Math.sin(double angle)
Cosine	$\cos \theta = \dfrac{x}{r}$	double Math.cos(double angle)
Tangent	$\tan \theta = \dfrac{y}{x}$	double Math.tan(double angle)
Arcsine	$\arcsin \dfrac{y}{r} = \theta$	double Math.asin(double ratio)
Arccosine	$\arccos \dfrac{x}{r} = \theta$	double Math.acos(double ratio)
Arctangent	$\arctan \dfrac{y}{x} = \theta$	double Math.atan2(double y, double x)
Pythagorean theorem	$r = \sqrt{x^2 + y^2}$	double Math.hypot(double x, double y)

Note that the tangent function has a period of $\pi$, instead of $2\pi$ (the period of the sine and cosine functions). Thus, in order to properly distinguish between $\theta$ values across the full $\left[0, 2\pi \right)$ interval, the Math.atan2 method takes both y and x as parameters, rather than just the ratio of the two. This also gives us a clean way to evaluate the arctangent in cases where the ratio is not finite (e.g. for $\theta = \pi /2$ and $\theta = 3\pi /2$).